Equilibrium point defect and charge carrier concentrations in a material determined through calculation of the self-consistent Fermi energy
Abstract
A concise procedure to determine the self-consistent Fermi energy and defect and carrier concentrations in an extended crystalline system is presented. It is assumed that the formation enthalpies of a set of variously charged point defects in thermodynamic equilibrium are known, as well as the density of electronic states in the defect-free system. By applying the constraint of overall charge neutrality, the self-consistent Fermi energy is determined using an iterative searching routine. The procedure is incorporated within a Fortran code ‘SC-FERMI’: the input consists of the defect formation energies, density of sites where they can form, and the degeneracy of each charge state; the material band gap; and the calculated density of states of the pristine system. The output is the self-consistent Fermi energy, the total concentrations of each defect as well as the concentration of its individual charge states, and the free carrier concentrations. Furthermore, the procedure facilitates fixing the concentration of one or more defects and determining the resulting self-consistent Fermi energy and concentrations of other defects (performed using the related code ‘FROZEN-SC-FERMI’), thus modelling `frozen-in’ defects which may form by kinetic, rather than thermodynamic, processes. One can fix the total concentration or the concentration of a particular charge state; it is also possible to introduce new defects with a fixed concentration, but here the charge state must be specified. The background theory is discussed in some detail, and the operation of the program is demonstrated by some examples.
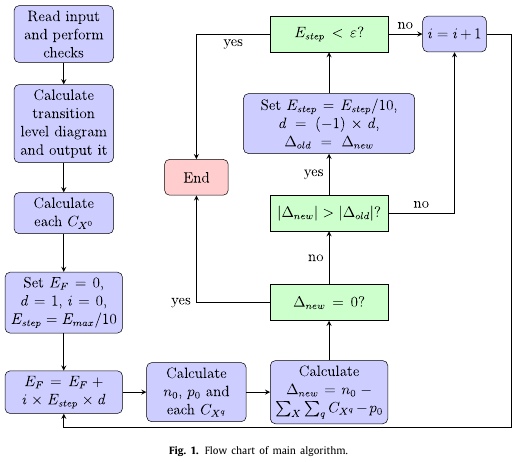
This paper describes the algorithm for my code SC-FERMI, which allows you to compute the self-consistent Fermi energy for a system with a set of defects. The operation of the code is demonstrated using the set of intrinsic point defects in GaN calculated using hybrid QM/MM. As those calculated defect levels were a bit controversial at one stage, I showed that the values used are actually quite similar to other calculations in the literature using plane-wave density functional theory. I had fun deriving the defect concentration expressions from statistical mechanics!
John Buckeridge
Lecturer in Energy Engineering and Materials Devices
Materials physicist working at the School of Engineering - Division of Electrical and Electronic Engineering, London South Bank University.